Modelling approaches for layered rocks
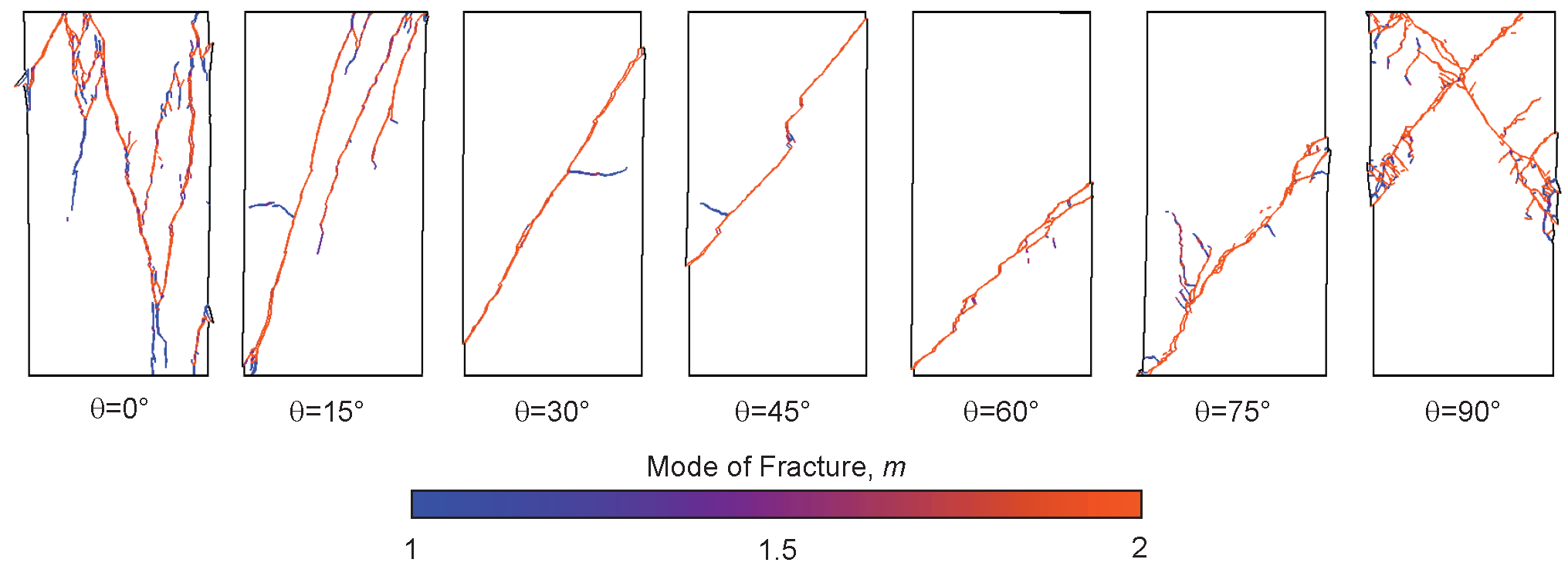
Mechanical anisotropy: sources and implications The mechanical behaviour of several rocks, such as schists, sandstones, shales and basalts, is characterized by strong stiffness and strength anisotropy . This anisotropy may arise at different spatial scales…